|
摘要:采用数值模拟的方法,对比研究了不同环量指数的轴流风扇在设计工况下的气动性能,通过分析风扇内部流动结构,揭示了沿叶高变环量设计对气动性能影响的控制机理。结果表明:环量指数取适当的负值时,风扇叶顶通流能力较强,削弱了间隙处逆流对主流的影响,减小叶顶间隙泄漏带来的损失;但环量指数若取值过小,会使吸力面根部沿径向指向叶顶和沿轴向指向前缘的静压梯度较大,促进了附面层的分离,增大了二次流动损失。本文的轴流风扇在环量指数取-0.2左右时气动性能最好。
关键词:轴流风扇;变环量设计;扭叶片;气动性能;叶顶间隙
中图分类号:TH432.1 文献标志码:B
Mechanism Analysis of Aerodynamic Performance for Axial Flow Fan Based on Circulation Distribution
Abstract: In the present paper, the aerodynamic performance of axial flow fan with different circulation index at a design flow rate is shown, and the internal flow characteristics is also discussed and analyzed by numerical simulation method. Results indicate that when circulation index takes an appropriate negative value, the stronger flow capacity of blade tip could weaken the influence of gap reflux on the mainstream, reducing the tip leakage loss, but if the value of circulation index is too small, it will exist larger static pressure gradient on suction surface in blade root which points to the blade tip along the radial and points to the leading edge along the axial direction, prompting the boundary layer separation, increasing the secondary flow loss. When circulation index takes -0.2, the axial flow fan makes its best aerodynamic performance.
Key words: axial flow fan; variable circulation design; twisted blade; aerodynamic performance; tip clearance
0 引言
轴流风扇是一种使用广泛的流体机械,高效、低噪及稳定工况范围宽的轴流风扇是研究的热点问题。轴流风扇设计的研究主要集中在两个方向,一是研究叶片径向扭曲[1] 、周向弯曲[2]及轴向倾掠[3]等对性能的影响;二是研究轴流风扇的多点多目标优化[4-6] 。叶片扭曲是控制气流参数沿叶高变化的有效手段,其中指数形式的环量分布方法[7]因其简洁的形式和灵活多样的分布,在低速风扇的扭叶片设计中得到广泛的使用。
对于无前置导叶的轴流风扇,气动负荷大小正比于叶轮后的环量分布。刘红蕊等[1]研究了不同载荷展向分布规律对轴流风扇性能的影响,结果表明:在叶根若负荷过大,则气流过度折转容易造成分离,而在叶顶若负荷过大,也易增强叶顶泄漏流,适当减小叶根和叶顶的负荷可以提高风机的性能。Bonaiuti等[4]采用反问题设计三维叶片, 选取环量分布作为优化自变量, 优化了单级轴流压气机。Kyoung-Yong Lee等[5]则运用实验设计与数值模拟的方法先筛选出对风扇气动性能影响较大的几何参数,然后将这些参数作为优化因素用响应面方法进行寻优,优化后的风扇静压提升了28.2%。这些结果也说明,控制环量分布对优化轴流风扇的性能是很有价值的。
本文应用数值模拟的方法,对比不同环量指数下风扇气动性能,通过分析内部流动结构,并着重分析叶顶间隙的流动情况,揭示环量分布对轴流风扇性能影响的机理。
1 轴流风扇的气动设计
本文采用CLARK-Y叶型,参照孤立叶型理论[7]采用变环量流型设计方法,设计了一组轴流风扇,设计参数见表1。
|
|
|
其中:ηt为全压效率;ω为叶轮角速度;C为叶型升力系数;b 为叶型弦长;z为叶片数,wm为来流平均相对速度。
|
|
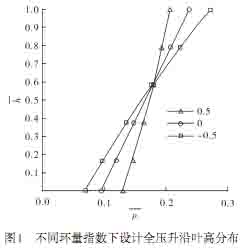 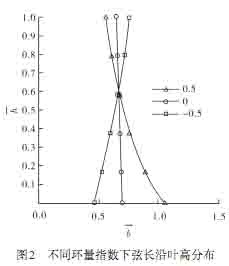
|
|
从图1、图2可以看出:1)α=-0.5是把设计全压集中在叶顶,以充分利用叶顶的高线速度,而α=0.5相当于减小叶顶处的设计全压,并将其转移到叶根;2)当α改变时,叶根弦长比叶顶弦长变化得更加剧烈。特别的,当α=0.5时叶根弦长是叶顶弦长的两倍还多,这会导致叶片扭得特别厉害。
2 数值分析方法与验证
采用FINE-TURBO软件对变环量设计的一组叶轮进行了模拟计算。风扇流道进口加半球形导流罩。叶顶间隙高度为3mm。在叶片近壁面、轮毂及叶顶间隙、头尾缘等复杂流动区域进行了网格局部加密处理,网格总数为65万。
|
|
|
计算过程中的湍流模型为Spalart-Allmaras(S-A)模型,空间离散采用Jameson有限体积中心差分格式,时间推进采用显式四阶Runge-Kutta法。
为了验证数值模拟的准确性,作者将环量指数为0.5的风扇做出实物模型,按照风室法GB1236-2000标准进行了实验测试。结果对比见图4。
实验结果的静压效率计算公式为:
η=pQ/3600(N-N0)
其中p为进出口静压差,Pa;Q为体积流量,m3/h;N为电机的输入功率,W;N0为无负载时,轴系的空转功率。
|
|
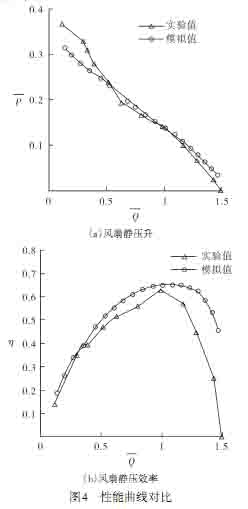
图中的静压升系数、流量系数的定义为:
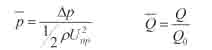
|
式中:Q0代表设计流量;Utip为叶尖旋转线速度。
图4a数值模拟的流量-静压曲线与实验结果趋势基本一致;从图4b流量-静压效率曲线可以看到,数值模拟的结果比实验结果偏高,相差的原因可能在于数值模拟仅针对风扇转子进行,未包含测试平台的进口集流器、出口扩散筒和消声层等结构部件。在大流量时,由于风室静压值较低,实验测量精度的限制和数值结果的相对误差就比较大。但总体上看,在设计工况点,数值模拟的风扇性能是准确的,而在大流量工况范围,静压效率相差5%以内。本文数值模拟方法预测评价风扇性能是可靠的。
3 环量指数的影响
图5为设计流量下,风扇静压升、静压效率随环量指数的变化曲线。
|
|
|
|
随着环量指数α从0.7开始减小,静压升在增大的同时,效率也在不断的提高;环量指数α减小到-0.2时,静压效率取得最大值,此后静压升和静压效率都开始一定幅度的减小。
无论从压升还是效率上看,当环量指数取一定的负值(-0.2~0)对本文所要研究的轴流风扇是有利的,特别在α=-0.2时,取得最佳效率点,此点较α=0.5的测试风扇静压升高出3.1Pa、静压效率高出4.6%,这说明选择合适的环量指数在轴流风扇的设计中有着重要的意义。
下文取实验测试的风扇(α=0.5)、最高效率点的风扇(α=-0.2)以及较小环量指数的风扇(α=-0.7)来进行内部流动对比分析。
4 风扇内部流动结构
|
|
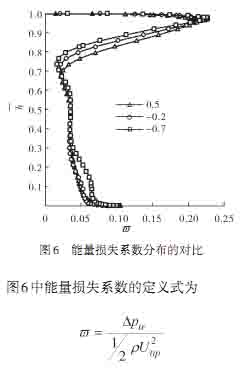
|
其中:Δptr进出口相对总压差,可以看出,损失主要集中在叶顶区域(70%~95%叶高),这是由叶顶间隙导致的泄漏流动引起的(见图7),而且在环量指数从0.5减小到-0.7的过程中,叶顶间隙区域的损失是不断减小的。
图7中可以看到间隙泄漏的流体在间隙通道内由于受到进出口压差的作用而产生逆流,沿机闸流动到进口,并与来流掺混形成漩涡。这个漩涡使叶轮进口处截面变窄,阻塞了流道,对流动极为不利。图8中相对速度系数定义式为: G=W/Utip(w为相对速度的大小),结合漩涡区速度流线以及相对速度系数云图可以看到,α=-0.7时,漩涡区域的范围是最小的。
|
|
|
|
图9为风扇出口密流在叶高上的分布,密流的定义式为:Φ=ρcz,它表征了流道内通流能力的大小。从图9中可以看出,由于α=-0.7风扇叶顶负荷较大、做功能力强,使其叶顶区域的通流能力要强于其他两个风扇,较强的通流能力削弱了间隙处逆流流体对主流的影响,从而减小因间隙泄漏产生的逆流所带来的损失。
|
|
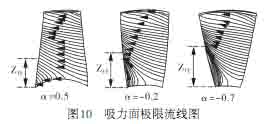
|
图10为三个风扇吸力面极限流线图,图中标注的尾缘处径向流动发展高度ZTE表征了这三种情况下端壁二次流动发展的范围[8] 。可以看到:随着环量指数从0.5减小到-0.7,径向高度ZTE是不断增大的,这意味着二次流动影响的范围越来越大;而且环量指数减小时,根部弦长的不断缩短使得二次流动在轴向的发展也变得格外迅速,以至于α=-0.7时叶高中间尾缘处流线出现一定的集结。α=-0.7风扇根部比较剧烈的二次流动导致了流场的恶化,使二次流动损失迅速增大,这就解释了图6中α=-0.7风扇根部损失大于其它两者的原因。
|
|
|
|
图11中横坐标Cax为无量纲弧长(弧长与叶高H的比值);纵坐标Cp为叶片表面静压力系数。观察α=0.5风扇10%和50%叶高的吸力面静压系数分布可以发现,两条曲线出现了交叉,在交叉点之后,50%叶高静压高于10%叶高,静压梯度由50%叶高指向10%叶高(箭头所示),这个径向静压梯度可以降低近壁面的径向窜流,抑制二次流动的发展。α=-0.2风扇,交叉点后移,由50%叶高指向10%叶高的静压梯度的范围减小。α=-0.7风扇的10%和50%叶高吸力面静压系数曲线已经不再相交,在从前缘至尾缘的整个弧长范围内,静压梯度由10%叶高指向50%叶高,这加速了附面层在径向的发展,使二次流动损失增加。
|
|
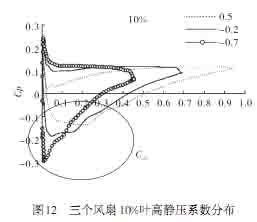
|
图12把三个风扇10%叶高静压系数分布放在一起作对比,可以分析出它们轴向的静压梯度差异。三个风扇吸力面静压沿轴向都是急剧减小后又逐渐增大,这意味着贴近吸力面流体沿轴向是先加速流动后减速流动,在后半段存在一个由尾缘指向前缘的静压梯度,这个静压梯度促使了吸力面附面层的分离。图中圈出了三个环量指数风扇吸力面静压最小值点的位置,可以发现α=-0.7风扇此点最低、静压值最小,而它轴向的尺寸又最短,这就导致了α=-0.7风扇轴向的静压梯度最大,进一步促使了附面层的分离。
5 结论
利用CFD方法对低压轴流风扇的流场进行了模拟,通过给定不同的环量指数,研究了环量指数对内部流动及损失分布的影响。针对本文设计研究的低压轴流风扇,可以得到以下的结论:
1) 间隙的存在使风扇损失集中在叶顶,环量指数取适当的负值时,风扇叶顶处通流能力较强,可以削弱逆流漩涡对主流的影响,减小叶顶间隙泄漏带来的损失。
2) 环量指数如果取值过小,会使根部吸力面沿径向指向叶顶和沿轴向指向前缘的静压梯度都较大,促使了附面层的分离,增大了二次流动损失。
3) 本文所研究的轴流风扇在环量指数α=-0.2时,气动性能要优于α=0.5,静压效率提升了4.6%。
参 考 文 献
[1] 刘红蕊,耿少娟,聂超群,等. 对旋式轴流风扇变环量流型的改进设计[J]. 风机技术, 2011(3):34-38.
[2] 欧阳华,李杨,杜朝辉,等. 周向弯曲方向对弯掠叶片气动─声学性能影响的实验研究 [J]. 航空动力学报, 2006,21(3) :668- 674.
[3] 杨爱玲,唐涛,张辉,等. 掠动叶对微型轴流风扇气动-声学性能的影响研究[J]. 工程热物理学报, 2009(3):411-414.
[4] Bonaiuti D, Zangeneh M. On the coupling of inverse design and optimization techniques for the multi-objective, multi-point design of turbomachinery blades[J]. Journal of Turbomachinery, 2009, 131(2): 021014.
[5] Kyoung-Yong Lee, Young-Seok Choi, Young-Lyul Kim and Jae-Ho Yun . Design of axial fan using inverse design method.[J]. Journal of Mechanical Science and Technology 22 (2008) 1883~1888
[6] 何柳,单鹏. 基于环量分布的轴流双级风扇三维数值优化[J]. 航空动力学报, 2010,(12):2660-2672.
[7] 李庆宜主编. 通风机[M]. 北京:机械工业出版社,1981.
[8] 叶大均, 周礼蔚. 涡轮叶栅二次流损失的实验研究[J]. 工程热物理学报, 1985(2):130-135.
|